Las matemáticas son una locura. Si bien los conceptos básicos son bastante simples, la filosofía detrás de algunos de estos fundamentos muy simples puede ser bastante profunda ... e incluso desconcertante. Hoy vamos a ver todo, desde los números primos hasta el infinito. ¡Así que prepárate porque estos son 25 principios matemáticos extraordinarios para desafiar tu cerebro!
La cuerda del ecuador
 Fuente: abc.net.au, Imagen: pexels (dominio público)
Fuente: abc.net.au, Imagen: pexels (dominio público) Si envolvieras una cuerda alrededor del ecuador de la Tierra para que se abrazara firmemente al suelo, solo necesitarías agregar unos 6, 3 metros de cuerda para que todo se balancee a 1 metro sobre el nivel del suelo (en todo el contorno del Tierra). Este resultado contrario a la intuición funciona sin importar cuán grande sea la esfera. La manera más simple de explicar esto es recordar que la circunferencia es igual al diámetro por pi. Esto significa que si desea que la cuerda se desplace un metro por encima de la Tierra, solo necesita aumentar el diámetro en 2 metros (1 metro en cada extremo del globo). Por lo tanto, solo necesitaría aumentar la circunferencia de la cuerda en 2 x pi metros (6.28318530718 metros).
Hippasus de Metapontum
 Fuente: esoterx.com, Imagen: https://commons.wikimedia.org (dominio público)
Fuente: esoterx.com, Imagen: https://commons.wikimedia.org (dominio público) El hombre que demostró que existían números irracionales fue asesinado por ello. Su nombre era Hippasus de Metapontum, y sucedió alrededor de 520 aC Pitágoras y muchos matemáticos griegos de la época creían que todos los números eran enteros o enteros. Fue cuando Pitágoras estaba realizando sus famosos cálculos de triángulo (teorema de Pitágoras) que tropezó con la raíz cuadrada de dos. Para abreviar, presuntamente trató de mantener secreto su hallazgo y se volcó cuando Hippasus lo publicó.
Números de Munchausen
 Fuente: zach.se
Fuente: zach.se Además de hacer algunas suposiciones sobre 0 ^ 0, 3435 es el único número además de 1 en el que puede dividir cada dígito, aumentarlo por su propia potencia, sumarlo todo y recuperar el mismo número. Básicamente, 3 ^ 3 + 4 ^ 4 + 3 ^ 3 + 5 ^ 5 = 3435 Nota: 438579088 también funciona si supone que 0 ^ 0 = 0. Estos se llaman números de Munchausen.
La representación decimal del 7mo
 Imagen: https://pixabay.com (dominio público)
Imagen: https://pixabay.com (dominio público) Las representaciones decimales del 7mo son el mismo conjunto de números que se repiten, excepto que siempre comienzan desde un punto diferente. 1/7 = 0.142857142857 ... y 2/7 = 0.285714285714 ... y 3/7 = 0.428571428571 ...
Conteo binario de dedos
 Fuente: mathisfun.com, Imagen: https://pixabay.com (dominio público)
Fuente: mathisfun.com, Imagen: https://pixabay.com (dominio público) Si usas binario, puedes contar hasta 1023 en tus dedos.
10!
 Fuente: reddit.com
Fuente: reddit.com ¡Hay exactamente 10! segundos en 6 semanas. Es más fácil ver esto cuando lo descompone como tal: 6 * 7 * 24 * 60 * 60 = 6 * 7 * (8 * 3) * (3 * 2 * 10) * (1 * 3 * 4 * 5) = 6 * 7 * 8 * 9 * 2 * 10 * 1 * 3 * 4 * 5 = 10!
El número de Graham
 Fuente: ibmathresources.com, Imagen: https://pixabay.com (dominio público)
Fuente: ibmathresources.com, Imagen: https://pixabay.com (dominio público) El número de Graham es tan grande que si escribes cada dígito lo más pequeño que puedas, aún ocupará más espacio de lo que está disponible en el universo observable. De hecho, si pudieras tener todos los dígitos en tu cabeza, tu cerebro colapsaría en un agujero negro (debido a la densidad astronómica de las conexiones neuronales que necesitarías).
Repetir decimales
 Imagen: https://pixabay.com (dominio público)
Imagen: https://pixabay.com (dominio público) Cualquier decimal que se repita se puede escribir como una fracción sobre un número equivalente de 9 (como la parte que se repite). Por ejemplo, .456456456 ... sería 456/999
Barajar cartas
 Fuente: qi.com, Imagen: https://www.pexels.com (dominio público)
Fuente: qi.com, Imagen: https://www.pexels.com (dominio público) Cada vez que baraja aleatoriamente un mazo de 52 cartas, casi seguramente las ha dispuesto en un orden completamente único. Lo que queremos decir con esto es que en toda la historia de la humanidad, nadie ha barajado una baraja de la misma manera. ¿Cómo? Bueno, ¡hay 52! formas en que puede ordenar el mazo (52 * 51 * 50 ...) Esto lleva a 8.0658 x 10 ^ 67 posibilidades. En comparación, el universo tiene solo 1 x 10 ^ 18 segundos de antigüedad. Incluso si barajas una baraja cada segundo desde el big bang ... aún te quedarías miserablemente corto.
La botella de Klein
 Fuente: math.union.edu
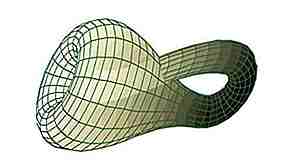
Fuente: math.union.edu Si toma dos tiras de Möbius y extiende los bordes para que se conecten (en efecto, pegándolos), crea una botella de Klein. Esta "botella" es un ejemplo de una superficie no orientable. Básicamente, existe solo en 4 dimensiones, pero se puede representar libremente en 3. Al igual que la tira de Möbius, tiene solo 1 superficie, pero no bordes. Es bastante truculento.
El teorema frívolo de la aritmética
 Fuente: mathworld.wolfram.com, Imagen: https://pixabay.com (dominio público)
Fuente: mathworld.wolfram.com, Imagen: https://pixabay.com (dominio público) El Teorema de la Aritmética Frívola afirma que, debido a que es infinito, la gran mayoría de los números naturales son muy, muy grandes.
Lo que se encuentra entre 0 y 1

Hay una cantidad infinita de números entre 0 y 1 (y 1 y 2, etc.). Por ejemplo, ½, ⅓, ¼, y puedes seguir adelante.
Números no computables
 Fuente: igoro.com, Imagen: http://www.pixnio.com (dominio público)
Fuente: igoro.com, Imagen: http://www.pixnio.com (dominio público) Casi todos los números reales son irracionales. Aún más, la mayoría de los números irracionales ni siquiera son computables. Y para asombrar tu mente, cada número que hayas visto en tu vida es computable, incluyendo infinitos números repetitivos como pi (porque puedes crear un algoritmo para calcularlo). Entonces, para decirlo simplemente, hay una cantidad infinita de números que nunca veremos (de hecho ... la mayoría de ellos) porque no tenemos forma de calcular esos números. En cierto sentido, son la "materia oscura" de las matemáticas. Sabemos que están ahí y que constituyen la mayoría incalificable de los números, pero no tenemos forma de llegar a ellos. Nota: la constante de Chaitin es un ejemplo de número no computable, pero desafortunadamente ... no es computable.
Los diferentes tipos de infinito
 Fuente: math.brown.edu, Imagen: https://pixabay.com (dominio público)
Fuente: math.brown.edu, Imagen: https://pixabay.com (dominio público) Aunque los números enteros son infinitos, hay infinitos más números reales que enteros. ¿Cómo puede ser eso si los enteros ya son infinitos? Es porque hay dos tipos de infinito ... contables e incontables. Los enteros son infinitamente contables, mientras que los números reales no (debido a que también incluyen los números irracionales). Entonces esto lleva a algunas conclusiones locas. El número de enteros positivos (0, 1, 2, ...) es exactamente el mismo que el número de enteros positivos y negativos combinados (..., -3, -2, -1, 0, 1, 2, 3, ...). Aunque estos dos conjuntos infinitos son iguales, son ambos más pequeños que el conjunto infinito de números reales. De hecho, hay infinitamente más números entre solo dos enteros aleatorios (0 y 1 por ejemplo) que los que existen en el conjunto infinito entero de enteros.
Los números normales
 Fuente: mathworld.wolfram.com
Fuente: mathworld.wolfram.com Un número normal es básicamente un número irracional que no tiene más de un dígito dado que otro. Entonces, por ejemplo, en el número 4.56856948576434 ... cada dígito debería aparecer aproximadamente la misma cantidad de veces hasta el infinito. Aunque hay pruebas aproximadas de que la mayoría de los números reales son normales, y sospechamos que números como pi y e son normales, todavía no hemos podido mostrarlo.
Los números trascendentales
 Fuente: mathworld.wolfram.com
Fuente: mathworld.wolfram.com Aunque casi todos los números reales y complejos son trascendentales (en oposición a los algebraicos, que básicamente son cualquier número que sea la raíz de un polinomio), solo hay unos pocos que se conocen, principalmente porque es realmente difícil demostrar que un número es trascendental. Los números trascendentales más conocidos son e y pi.
El primer solitario
 Fuente: mathworld.wolfram.com, Imagen: https://commons.wikimedia.org (dominio público)
Fuente: mathworld.wolfram.com, Imagen: https://commons.wikimedia.org (dominio público) Cada número primo único hasta el infinito es extraño. Excepto por 2.
El efecto del infinito en la probabilidad
 Imagen: https://pixabay.com (dominio público)
Imagen: https://pixabay.com (dominio público) El concepto de infinito tiene algunos efectos locos sobre la probabilidad. Si tuviera que seleccionar aleatoriamente un número real, la probabilidad de que sea racional (1, 2, ¾, 78/56, ...) es 0. Esto se debe al hecho de que los números irracionales son incontables infinitos, mientras que los números racionales son infinitamente contables. Y, el infinito contable sobre infinito incontable es 0.
.999 ... = 1
 Imagen: https://commons.wikimedia.org (dominio público)
Imagen: https://commons.wikimedia.org (dominio público) .999 ... es igual a 1. En este punto, tu mente probablemente esté tan turbada con el concepto de infinito que probablemente solo aceptes lo que te digamos, pero lo probaremos. Sabes que .333 ... es igual a ⅓ y .666 ... es igual a ⅔. ⅓ + ⅔ = 1 y .333 ... + .666 ... = .999 .... Otra forma de pensar en esto es que si .999 ... no es igual a 1, debería haber algún número entre .999 ... y 1. Lo cual, gracias al concepto de infinito, no lo es.
La función de Dirichlet
 Fuente: mathworld.wolfram.com
Fuente: mathworld.wolfram.com De acuerdo con la función de Dirichlet, entre dos números irracionales hay un número racional. La parte loca? Hay números infinitamente más irracionales que los números racionales (como establecimos previamente). Entonces ... ¿cómo podría cada dos números irracionales tener un número racional entre ellos? Esperaría quedarse sin números racionales. Pero el infinito simplemente no se comporta de la manera que esperábamos.
Identidad de Euler
 Fuente: mathworld.wolfram.com
Fuente: mathworld.wolfram.com La identidad de Euler se cita a menudo como un ejemplo de belleza matemática. Es e ^ (pi * i) + 1 = 0. Contiene 5 de las constantes matemáticas más fundamentales 0, 1, e, pi e i. Además, tres de las operaciones aritméticas básicas ocurren exactamente una vez: suma, multiplicación y exponenciación. Benjamin Peirce, un destacado matemático dijo una vez después de probarlo en una conferencia, "la identidad es absolutamente paradójica; no podemos entenderlo, y no sabemos lo que significa, pero lo hemos probado, y por lo tanto sabemos que debe ser la verdad ".
El problema de Monty Hall
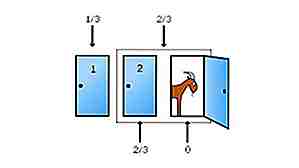 Fuente: mathworld.wolfram.com, Imagen: https://commons.wikimedia.org (dominio público)
Fuente: mathworld.wolfram.com, Imagen: https://commons.wikimedia.org (dominio público) El problema de Monty Hall es un famoso ejemplo de cómo la probabilidad puede ser contraintuitiva. Digamos que en un concurso de juegos hay tres puertas. Detrás de uno de ellos hay un auto, mientras que los otros dos están escondiendo cabras. Eliges abrir la puerta 1. Sin embargo, el anfitrión sabe qué hay detrás de las puertas. Abre la puerta 3 para revelar una cabra. Ahora él le pregunta si le gustaría cambiar su elección a la puerta 2. ¿Qué hace? La respuesta es que debes cambiar tu elección. ¿Por qué? Debido a que al cambiar a la puerta 2 tiene una probabilidad de ganar el automóvil mientras permanece en la puerta 1, tiene una posibilidad áspera. La mejor forma de visualizar esta solución contraintuitiva es aumentar el número de puertas. Digamos ahora que hay 100 puertas. Eliges la puerta 37. El anfitrión ahora abre todas las puertas para revelar las cabras a excepción de la puerta 83. ¿Quieres cambiar tu selección del 37 al 83? ¿O te quedarías en 37? El hecho es que sus posibilidades de ganar el automóvil aumentarán significativamente al cambiar a la puerta 83.
La diferencia entre 1 millón y 1 billón

Un millón de segundos es alrededor de 11 días y medio. Mil millones de segundos es justo por debajo de los 32 años.
El Principio de Pigeonhole
 Fuente: mathworld.wolfram.com, Imagen: https://commons.wikimedia.org (dominio público)
Fuente: mathworld.wolfram.com, Imagen: https://commons.wikimedia.org (dominio público) Si tiene 2 tipos de calcetines en su cajón y agarra aleatoriamente 3 sin mirar, tiene la garantía de tener un par correspondiente. Mientras que para algunas personas esto es obvio, para otros puede ser más difícil de entender. Se basa en algo llamado principio de casillero. Básicamente, si tienes n tipos de algo, entonces necesitas elegir aleatoriamente n + 1 de esa cosa para obtener una coincidencia. Entonces, si tiene 5 tipos diferentes de calcetines en su cajón y agarra aleatoriamente 6 de ellos ... está garantizado que tendrá una coincidencia. ¡Esto puede ser genial para vestirse en la oscuridad!
La suma de todos los enteros positivos desde 1 hasta el infinito
 Fuente: ver a continuación, Imagen: https://commons.wikimedia.org (dominio público)
Fuente: ver a continuación, Imagen: https://commons.wikimedia.org (dominio público) Ahora, prepárate para la cosa más alucinante que puedas escuchar en toda tu vida. Si suma todos los enteros positivos de 1 a infinito ... ¿qué obtiene? ¿Supiste -1/12? Porque esa es la respuesta correcta. Sabemos. Esto suena absolutamente ridículo y hasta cierto punto lo es. ¿Por qué? Porque agregar algo hasta el infinito es imposible y seguro arrojar resultados ridículos. Para hacer las cosas aún más locas para ti, este resultado es muy bien conocido en física, particularmente en la teoría de cuerdas. De hecho, si todavía no puede creer esto, le sugerimos que vea este video de los físicos Tony Padilla y Ed Copeland de la Universidad de Nottingham. Explican la locura mejor que nosotros: https://www.youtube.com/watch?v=w-I6XTVZXww.
Nota: el resultado se debe principalmente al hecho de que el infinito desafía nuestras expectativas. Infinity no es un número, es un concepto. Cosas como la suma y la resta no funcionan igual cuando involucras el infinito (tipo de cómo la física no funciona igual cuando te encuentras en medio de un agujero negro).
Más información: también vale la pena investigar la suma de Ramanujan y la serie de Grandi:
https://en.wikipedia.org/wiki/Ramanujan_summation
https://en.wikipedia.org/wiki/Grandi's_series
Otro recurso:
http://www.bradyharanblog.com/blog/2015/1/11/this-blog-probably-wont-help
Fotos: Imagen destacada: https://commons.wikimedia.org (dominio público), 20. pixel máximo, 16. Tttrung, Klein bottle2, CC BY-SA 4.0, 11. Mehran Moghtadaei, PP 1280 × 1024, CC BY- SA 3.0, 10. Stephen J. Brooks (hablar), Algebraicszoom, CC BY 3.0, 6. Judy Breck a través de flickr, CC BY-SA 2.0, 5. Quinn Dombrowski de Chicago, EE. UU., Identidad Graffito de Euler, CC BY-SA 2.0, 3. Cmglee, Visualización mil millones, CC BY-SA 3.0,




