25 simples trucos mentales de matemáticas que harán volar tu mente

Para ver si un número es divisible por tres, suma los dígitos. Si la suma es divisible por tres, también lo es el número. Nota: esto también funciona para 9.

x% de y es lo mismo que y% de x. Esto significa que si el 2% de 50 es demasiado difícil de descifrar, puedes voltearlo: 50% de 2. Eso es mucho más fácil.

Para multiplicar un número de 2 dígitos por 11, solo suma los dígitos y pega la respuesta entre ellos. Por ejemplo, 42 * 11 sería 4 + 2 = 6. Ahora coloque el 6 entre el 4 y el 2 para obtener 462.

Nota: No se olvide de llevar el 1. Para dar otro ejemplo, 58 * 11 sería 5 + 8 = 13. No se puede simplemente poner el 13 entre el 5 y el 8. Eso daría 5138, lo cual es obviamente incorrecto. Necesitas cargar el uno agregándolo al 5. Entonces sería 638.

Si necesita multiplicar un número por 5, puede ser más fácil hacerlo a la mitad y luego multiplicar por 10. Por ejemplo, 315 * 5 sería 315/2 = 157.5 Ahora solo mueva el decimal a multiplicar por 10 y obtenga 1575.

Para aproximar una raíz cuadrada, haga lo siguiente. Encuentra el siguiente cuadrado perfecto inferior. Agrégalo a tu número. Ahora divide por la raíz cuadrada del cuadrado perfecto inferior. Y ahora divide de nuevo por 2. Suena difícil? Aquí hay un ejemplo. Tome 31. El siguiente cuadrado perfecto más bajo es 25. Entonces 31 más 25 es 56. Ahora divida por la raíz cuadrada de 25. Entonces 56/5 = 11.2 Ahora divida por 2 para obtener 5.6

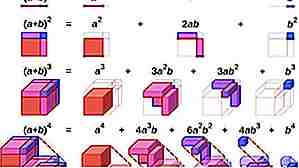
Use el teorema binomial (a + b) ^ 2 = a ^ 2 + 2ab + b ^ 2 para los números cuadrados. Por ejemplo 55 ^ 2 podría ser (50 + 5) ^ 2. Esto significa que 50 * 50 + 50 * 5 * 2 + 5 * 5 = 2500 + 500 + 25 = 3025.

Para ver si un número es divisible entre 8, verifique los últimos tres dígitos. Si son divisibles por 8, entonces el número es divisible por 8. Por ejemplo, 3423024 sería divisible por 8 porque 024/8 = 3

Para calcular una propina simplemente mueva el decimal un lugar a la izquierda para obtener el 10%. A continuación, agregue la mitad de lo que le queda para obtener el 15% o duplíquelo para el 20%. Por ejemplo, si la factura es de $ 43.21, entonces $ 4.32 es el 10%. La mitad de $ 4.32 es $ 2.16 así que si quieres 15% simplemente agrega eso. Te daría $ 4.32 + $ 2.16 = $ 6.48. Obtener 20% es aún más fácil porque solo lo duplicas. $ 4.32 * 2 = $ 8.64. Entonces, si se siente generoso, entonces $ 8.64 constituiría un 20% de propina.

Para calcular su salario anual, solo tome su salario por hora, duplíquelo y agregue 3 ceros. Supongamos que gana $ 8 por hora. Simplemente duplique eso por $ 16 y luego agregue tres ceros por $ 16, 000.

Para aproximar las conversiones entre Celsius y Fahrenheit simplemente multiplique por 2 y agregue 30 (yendo de C a F). Haz lo inverso para pasar de F a C (restar 30 y dividir por 2).

Para ver si un número es divisible por 4, solo mira los últimos dos dígitos. Si son divisibles por 4, entonces el número entero es divisible por 4. Entonces 23746316 sería divisible por 4 porque 16 es divisible por 4.

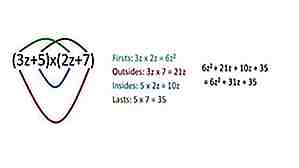
Para multiplicar dos números juntos, use el método FOIL (primero, exterior, interior, último). Por ejemplo, 25 * 37 sería (20) (30) + (5) (30) + (7) (20) + (5) (7) = 925.

Nota: esto es exactamente lo que haces cuando multiplicas en papel, es más fácil visualizar el método FOIL en tu cabeza.

Para calcular el porcentaje de un número (que no es el 10%) simplemente encuentre primero el 1% y luego multiplíquelo. Entonces, por ejemplo, 3% de 528 sería 528 * .01 = 5.28 (mueva el decimal dos lugares a la izquierda). Ahora solo multiplique por 3 para obtener 15.84

Esto funciona especialmente bien si uno de los números ya es bueno y redondo (termina en 0). Simplemente redondee el otro número, multiplique y ajuste el resultado en consecuencia. Por ejemplo, si desea calcular 18 * 30 no necesita el método FOIL que hicimos antes (porque 30 ya es bueno y redondo). Solo haz 20 * 30 que es 600 y luego resta dos 30 por 540.

Para verificar si un número es divisible entre 6, necesita combinar dos reglas de divisibilidad (dos y tres). Si es divisible por ambos, 2 y 3, entonces es divisible por 6. Ya hemos dividido por 3, pero por las dudas ... los números pares son divisibles por 2.

La representación decimal de los 11th se puede hacer multiplicando el numerador por 9 y simplemente repitiéndolo. Por ejemplo, 1/11 = .09090909 .... y 2/11 = .18181818 ... etc.

Para cuadrar cualquier número de dos dígitos que termine en 5, simplemente ponga 25 al final y multiplique el primer número por el siguiente dígito. Entonces, por ejemplo, 45 ^ 2 sería 2025 porque 5 es el siguiente dígito por encima de 4, entonces 4 * 5 = 20. Ahora solo ponga un 25 en el extremo para 2025.

Las representaciones decimales para las noventas son solo el numerador repetido. Por ejemplo 1/9 = .1111111 ... y 2/9 = .2222222 ... Esta es también una de las pruebas usadas para mostrar que .999999 ... = 1. (desde 9/9 = .99999 ...)

Para cuadrar números, un truco posible es sumar / restar del número hasta que obtienes dos números que puedes multiplicar fácilmente. A continuación, agregue la diferencia del número que agregó / restó. Para dar un ejemplo, 46 ​​^ 2 podría ser 42 * 50 porque 46 - 4 = 42 y 46 + 4 = 50. Entonces 42 * 50 sería 2100. Ahora cuadre el número que agregó / restó así que 4 ^ 2 = 16. Ahora agrega 16 para obtener 2116.

72 dividido por la tasa de interés le dará una estimación aproximada de cuántos años le tomaría duplicar su dinero (regla de 72).

Para hacer una adición mental, es mucho más fácil trabajar de izquierda a derecha en lugar de hacerlo de la forma en que lo haces en el papel (de derecha a izquierda). Esto se debe a que su cerebro reconoce y recuerda naturalmente los números comenzando por la izquierda. Por ejemplo, para hacer 376 + 581, agregue 300 + 500 para obtener 800. Ahora agregue 70 + 80, que es 150. Esto lleva el total a 950. Luego agregue el 7 para obtener 957. Básicamente, divida la adición en partes más pequeñas de izquierda a derecha. Otra ventaja de esto es que gradualmente irás a la solución. Por lo tanto, si solo quiere una aproximación, no tiene que esperar hasta que termine el problema para averiguar con qué orden de magnitud está trabajando (cientos, miles, etc.)

Para la resta mental, la idea es similar a la suma. Trabaja de izquierda a derecha, pero hay un truco adicional que debes tener en cuenta (sugerencia: se trata de redondear). Supongamos que quiere hacer 632 - 487. Primero, agregue 3 para redondear 487 al 10 más cercano, entonces 490. Ahora, el problema se convierte en 632 - 490. Esto es mucho más fácil. 632 - 400 es 232. Ahora restando 90 obtienes 142 (es 10 más que restar 100). A partir de ahí, solo recuerde volver a agregar el 3 desde el principio. Esto te da 145.

Otro truco para multiplicar números que se redondean fácilmente (generalmente termina en 8 o 9), es usar el método de resta. Para hacer esto, redondea el número y luego resta. Por ejemplo, 49 * 16 sería 50 * 16. Esto es mucho más fácil de resolver. Como 100 * 16 es 1600, puede obtener la mitad para obtener 800. Ahora recuerde restar lo que redondeó inicialmente. Entonces, como redondeaste 49 hasta 50, eso fue 1 * 16, que es lo que tienes que restar. Eso da 800 - 16 que es 784.

Recuerda que puedes hacer lo que quieras con una ecuación siempre que lo hagas en ambos lados. Además, puedes hacer lo que quieras con un término, siempre que lo estés multiplicando por uno. Tenga en cuenta que 1 tiene formas infinitas (2/2, (x-4) / (x-4), etc.).

Para convertir millas a kilómetros, puede obtener una estimación bastante cercana agregando 60%. La forma más rápida de hacerlo es agregar 50% y luego 10%. Por ejemplo. 60 millas en km serían las siguientes: 60 * .5 = 30 y 60 * .1 = 6. Ahora, 30 + 6 = 36. Agregue esto a 60 para obtener 96 km. Para ir de kilómetros a millas, solo resta 40%. Puedes hacer esto restando 50% y luego agregando 10%. Entonces, para obtener 350 km en millas, reste la mitad de 350. Eso le da 175. Ahora agregue nuevamente 10% de 350, que es 35. Esto lo deja con 210. Nota: tenga en cuenta que estas son estimaciones aproximadas. Cuanto más grandes sean tus números, más errores habrá.